农夫约翰有N（2<=N<=40000）个农场，标号1到N。M（2<=M<=40000）条不同的垂直或水平的道路连接着农场，道路的长度不超过1000.这些农场的分布就像下面的地图一样，图中的农场用F1~F7表示：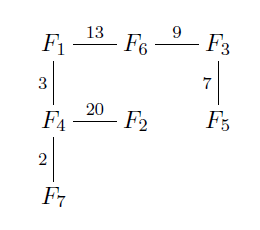

每个农场最多能在东西南北四个方向连接4个不同的农场，此外，农场只处在道路的两端。道路不会交叉且每对农场间有且仅有一条路径。邻居鲍勃要约翰来导航，但约翰丢了农场的地图，他只从电脑的备份中修复了每一条路的信息如下：

从农场23向南经距离10到达农场17

从农场1往东经距离7到达农场17

……

 
当约翰重新获得这些信息的时候，他有时会被鲍勃的问题打断：“农场1到农场23的曼哈顿距离是多少？”所谓（x1,y1）和（x2，y2）的“曼哈顿距离”就是|x1-x2|+|y1-y2|。如果已经有足够的信息，约翰就会回答这样的问题，否则他就会诚恳的道歉并回答-1。

第1行：两个分开的数N和M。

第2到M+1行：每行包括4个分开的内容，F1，F2，L,，D分别描述两个农场的标号，道路的长度，F1到F2的方向N,E,S,W。第x行表示时刻x-1知道的信息。

第M+2行：一个整数，K（1<=K<=10000），表示问题个数。

第M+3到M+K+2行：每行表示一个问题，由3部分组成：F1，F2，I，其中F1和F2表示两个被问及的农场，而I（1<=I<=M）表示问题提出的时刻。I为1时，表示现在的问题是时刻1提出的，时刻1在输入数据的第二行。

第1到K行：每行一个整数，回答问题，如果已知答案则回答两个农场间的曼哈顿距离，不知道答案就输出-1。